The noise in a silicon detector system plays an essential role, since the signals are very low. Especially with strip detectors, it is important to know each contribution to optimize the design. This is easier for pixel detectors, since their active area is very small and there is virtually no readout line impedance, which reduces many noise components down to negligible values compared to strip detectors.
The electronic noise in silicon detector systems is given in terms of
equivalent noise charge (ENC) referred to the input.
The main noise source is the input transistor in the amplifier, with a noise figure depending
on geometry and electrical parameters [24,31,34,35].
Noise contributions of further electronic stages are usually neglected.
Due to its integrating nature, the load capacitance plays an important role for the amplifier noise.
In a simple approach, the amplifier noise can be described by the sum of a constant
value (parallel noise) and a part which scales with the load capacitance ![]() (series noise),
(series noise),
Apart from the amplifier, there are other noise sources in the system. Fig.
![[*]](crossref.gif) shows noise related components in a typical AC coupled strip
detector configuration with a polysilicon bias resistor. The AC coupling capacitor can be
neglected in these considerations. The current source
shows noise related components in a typical AC coupled strip
detector configuration with a polysilicon bias resistor. The AC coupling capacitor can be
neglected in these considerations. The current source
Parallel noise sources are the constant part of the amplifier ![]() , leakage current
fluctuations
, leakage current
fluctuations
![]() and the polysilicon resistor noise
and the polysilicon resistor noise ![]() . The
capacitive fraction of the amplifier noise
. The
capacitive fraction of the amplifier noise ![]() and the readout line resistor noise
and the readout line resistor noise
![]() are series noise sources. As expected, the peaking time
are series noise sources. As expected, the peaking time ![]() plays an key role
in the noise functions. Numerical noise equations, in which the physical constants
are already expressed by numbers, can be written as
plays an key role
in the noise functions. Numerical noise equations, in which the physical constants
are already expressed by numbers, can be written as
| (2.36) | |||
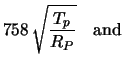 |
(2.37) | ||
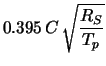 |
(2.38) |
| (2.39) |
The deconvolution method (see section ![[*]](crossref.gif) , p.
, p. ![[*]](crossref.gif) ) compromises the noise.
Both intrinsic amplifier noise components increase due to the signal processing and the
external series noise is amplified, while the parallel noise is reduced.
It has been shown [32,33] that the ratio between peak and deconvolution mode
noise can be expressed for parallel and series terms as
) compromises the noise.
Both intrinsic amplifier noise components increase due to the signal processing and the
external series noise is amplified, while the parallel noise is reduced.
It has been shown [32,33] that the ratio between peak and deconvolution mode
noise can be expressed for parallel and series terms as
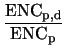 |
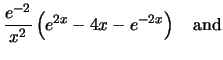 |
(2.40) | |
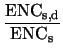 |
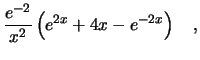 |
(2.41) |
To get a feeling for the magnitude of individual noise components, these figures
will be calculated and compared for the DELPHI Very Forward Tracker (VFT) [23]
and an average CMS silicon detector.
The VFT uses the MX6 readout chip, while the CMS strip detectors
will be instrumented with the APV25 described
in section ![[*]](crossref.gif) , p.
, p. ![[*]](crossref.gif) . The APV25 noise will be shown for both peak and deconvolution modes.
. The APV25 noise will be shown for both peak and deconvolution modes.
![[*]](crossref.gif) gives an overview of typical detector and readout parameters, while
the resulting noise contributions are shown in tab.
gives an overview of typical detector and readout parameters, while
the resulting noise contributions are shown in tab. ![[*]](crossref.gif) .
The dominant noise source of both detector systems is the amplifier chip, whose contribution
principally depends on the peaking time. It is obvious that the signal-to-noise-ratio (
.
The dominant noise source of both detector systems is the amplifier chip, whose contribution
principally depends on the peaking time. It is obvious that the signal-to-noise-ratio (The noise figures given here include the detector together with the input transistor of the front-end amplifier. In reality, other components in the read-out chain beyond this point also contribute to the total observed noise. Line drivers and receivers, the transmission line and the digitization typically add a few hundred electrons of noise. However, since this contribution is uncorrelated as well, the total square sum is still dominated by the front-end noise.