![\begin{displaymath}
-\frac{1}{\rho}\frac{dE}{dx}=4\pi N_{A} r^2_e m_e c^2 z^2 \f...
... \right) -\beta^2-\frac{\delta(\gamma)}{2}-\frac{C}{Z} \right]
\end{displaymath}](img67.gif) |
(2.1) |
The principle of solid state detectors is based on the energy loss of
traversing particles. Free electron-hole pairs are generated, which move towards
opposite electrodes under the influence of an electric field.
The energy loss of heavy particles in matter was described by
H.A.BETHE2.1and F.BLOCH2.2 [3].
![[*]](crossref.gif) represents the differential energy loss per mass
surface density
represents the differential energy loss per mass
surface density
However, in thin layers, the deposited
energy is less than expected because a fraction of the lost energy is carried
off by energetic knock-on electrons (also known as ![]() electrons).
These considerations lead to the restricted energy loss, which is expressed
by an additional term in the Bethe-Bloch equation [9],
electrons).
These considerations lead to the restricted energy loss, which is expressed
by an additional term in the Bethe-Bloch equation [9],
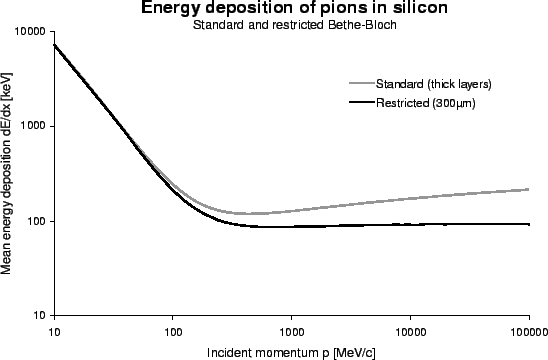 |
![[*]](crossref.gif) compares the standard Bethe-Bloch theory to the
restricted form for a pion traversing
compares the standard Bethe-Bloch theory to the
restricted form for a pion traversing The statistical fluctuation of the energy loss in thin layers was described by L.D.LANDAU2.3 [10]. The Landau distribution resembles a distorted normal distribution with a long upper tail due to rare, but highly ionizing knock-on electrons.
The tail of an ideal Landau distribution extends to infinite energies, which is unrealistic. In practice, the measurement range is always limited, which leads to a truncated Landau curve. As a result of its asymmetry, the mean energy loss is higher than the most probable (MP). However, the latter is much easier to obtain from measured data and therefore usually stated in experimental results. The scale factor between MP and mean is typically around 1.3 but depends on particle energy and measurement range.
With particle energies far below the MIP energy, corresponding to thick layers, knock-on electrons are improbable, the Landau tail vanishes and thus the resulting distribution is Gaussian2.4.
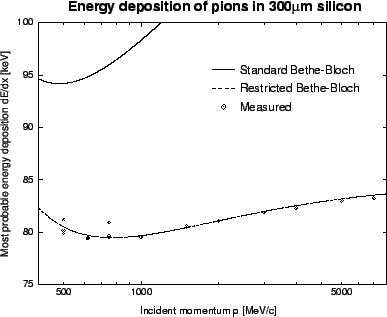
The restricted energy loss model has been confirmed by experiments, e.g. by
a dedicated test with silicon pad sensors at BNL performed in 1998 by HEPHY and
MIT, where excellent agreement between measurement and theory was found [11].
Fig. ![[*]](crossref.gif) shows the most probable energy loss of pions in the range of minimum
ionization in a silicon detector of
shows the most probable energy loss of pions in the range of minimum
ionization in a silicon detector of ![]() thickness.
thickness.
 |
The energy deposited in the detector material flows into the creation of free electron-hole
pairs. The number of pairs ![]() depends on the total energy loss
depends on the total energy loss ![]() and
the ionization energy
and
the ionization energy ![]() , which is necessary for a pair production,
, which is necessary for a pair production,
| (2.3) |
The measured energy loss distribution of MIPs in a typical silicon sensor (
![[*]](crossref.gif) in terms of the collected charge [12].
The measured data have been fitted by a Landau distribution, convoluted with a narrow normal
distribution due to electronic noise and intrinsic detector fluctuations [13].
This results in a minor broadening of the shape and a slight increase of the peak position
compared to pure Landau. As stated in the boxes on the right, the pure Landau
in terms of the collected charge [12].
The measured data have been fitted by a Landau distribution, convoluted with a narrow normal
distribution due to electronic noise and intrinsic detector fluctuations [13].
This results in a minor broadening of the shape and a slight increase of the peak position
compared to pure Landau. As stated in the boxes on the right, the pure Landau
Fig. ![[*]](crossref.gif) also illustrates why the MP is obtained much
easier than the mean value: Cuts on either end do affect the mean, but not the MP.
The low edge depends on the pedestal threshold, and the high edge is defined by
the range of the readout electronics. Moreover, nonlinearity and saturation
occur when measuring very high signals of the tail.
also illustrates why the MP is obtained much
easier than the mean value: Cuts on either end do affect the mean, but not the MP.
The low edge depends on the pedestal threshold, and the high edge is defined by
the range of the readout electronics. Moreover, nonlinearity and saturation
occur when measuring very high signals of the tail.
More experimental results, which confirm the theory of energy loss, are found in
section ![[*]](crossref.gif) , p.
, p. ![[*]](crossref.gif) .
.